Pareto Chart (Manufacturing Example)

The Pareto Chart is a tool used to rank the various categories/causes of a problem by charting them as bars in descending order of frequency or magnitude from left to right. It helps establish priorities by dividing the causes into the ‘vital few’ and the ‘trivial many’.

The theory behind the Pareto Chart originated in 1897 when an Italian economist named Vilfredo Pareto created a formula representing the uneven distribution of wealth - what later came to be known as the 80-20 rule.

You have probably heard a version of it like: "20% of the people cause 80% of the problems", or a derivative. Dr. J. M. Juran started applying this principal to defect analysis.

In fact, many (most) defect distributions follow a similar pattern, with a relatively small number of issues accounting for an overwhelming share of the defects.

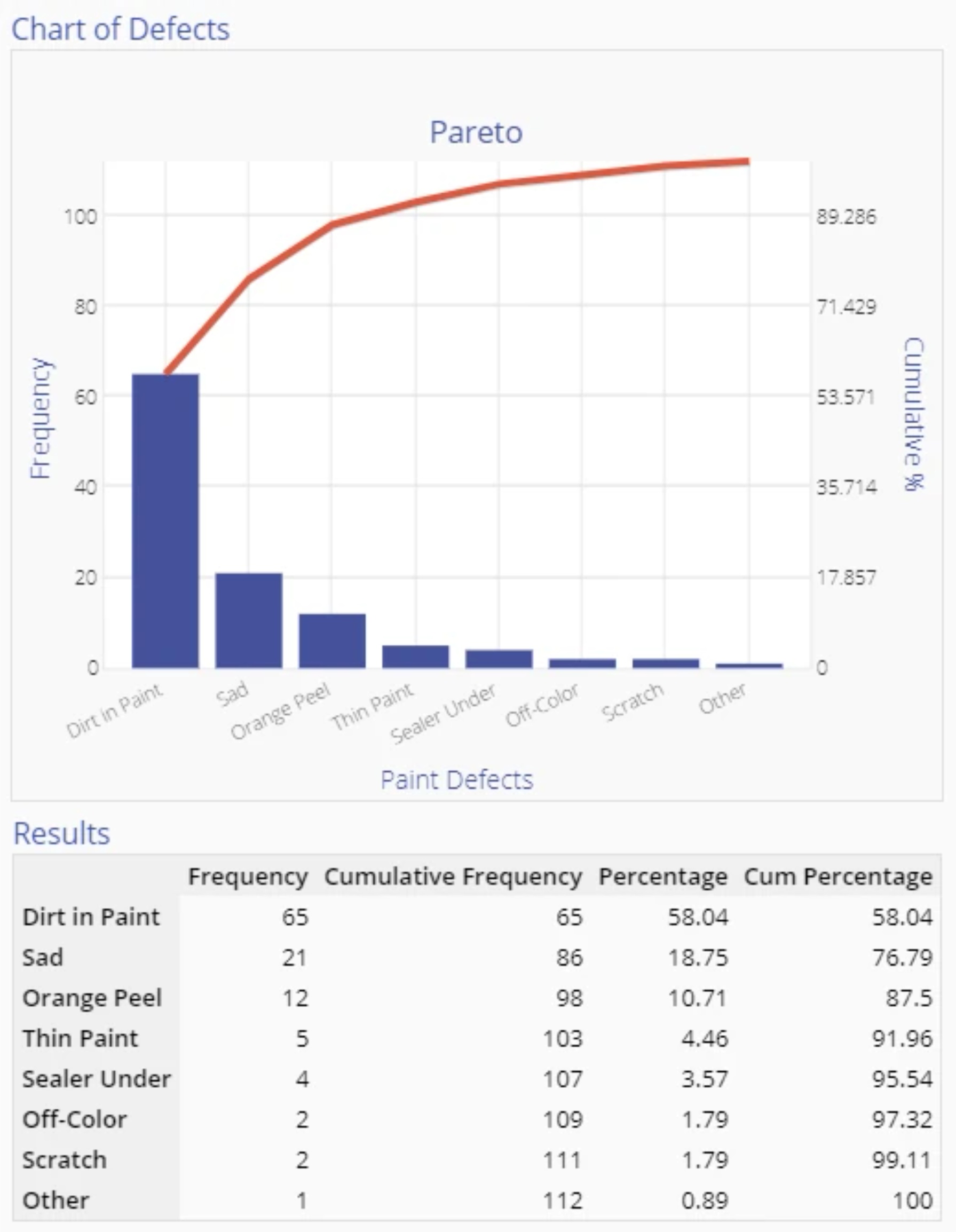
Following is an example of paint defects from an automotive assembly plant:

After reviewing the chart above, there is no question which defect to work on first. However, this Pareto Chart is constructed from one dimension only - defect frequency. If you learned that it costs $10 to fix a Dirt defect, while Sag defects cost $100 to correct, Sags would probably be the highest priority.

Likewise, if one category represents a constraint on the whole process, its priority would be elevated. You may wish to consult the Project Priority Calculator for a template to prioritize along multiple dimensions.

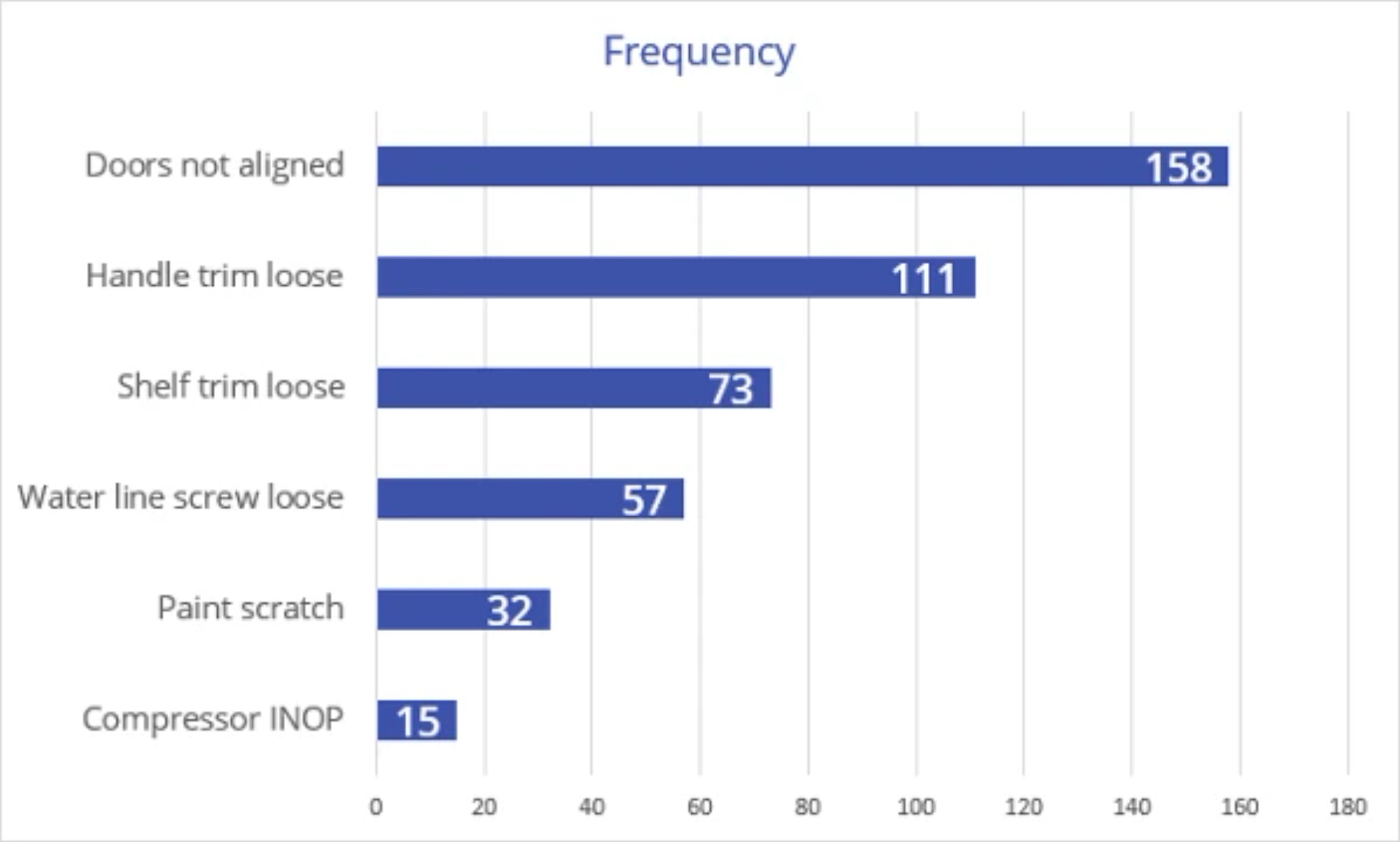
You can generate a Pareto Chart using virtually any spreadsheet or charting software. These charts were created using EngineRoom. Pareto charts are often constructed with horizontal bars, and without the cumulative percentage line, as shown below:

Summary

The Pareto Chart is a simple to use and powerful graphic to identify where the majority of problems in a process are originating. Using a Pareto Chart early in problem solving is an effective strategy to decrease project complexity.