Regression Analysis
Introduction
The regression analysis tool is an advanced tool that can identify how different variables in a process are related. The regression tool will tell you if one or multiple variables are correlated with a process output. This information can identify where in the process control is needed or what factors are the best starting point for a process improvement project.
As you develop Cause & Effect diagrams based on data, you may wish to examine the degree of correlation between variables. A statistical measurement of correlation can be calculated using the least squares method to quantify the strength of the relationship between two variables. The output of that calculation is the Correlation Coefficient, or (r), which ranges between -1 and 1. A value of 1 indicates perfect positive correlation - as one variable increases, the second increases in a linear fashion. Likewise, a value of -1 indicates perfect negative correlation - as one variable increases, the second decreases. A value of zero indicates zero correlation.
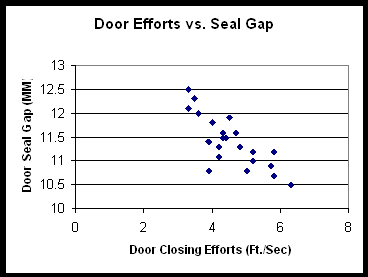
Before calculating the Correlation Coefficient, the first step is to construct a scatter diagram. Most spreadsheets, including Excel, can handle this task. Looking at the scatter diagram will give you a broad understanding of the correlation. Following is a scatter plot chart example based on an automobile manufacturer.
In this case, the process improvement team is analyzing door closing efforts to understand what the causes could be. The Y-axis represents the width of the gap between the sealing flange of a car door and the sealing flange on the body - a measure of how tight the door is set to the body. The fishbone diagram indicated that variability in the seal gap could be a cause of variability in door closing efforts.
In this case, you can see a pattern in the data indicating a negative correlation (negative slope) between the two variables. In fact, the Correlation Coefficient is -0.78, indicating a strong inverse or negative relationship.
MoreSteam Note: It is important to note that Correlation is not Causation - two variables can be very strongly correlated, but both can be caused by a third variable. For example, consider two variables: A) how much my grass grows per week, and B) the average depth of the local reservoir. Both variables could be highly correlated because both are dependent upon a third variable - how much it rains.
In our car door example, it makes sense that the tighter the gap between the sheet metal sealing surfaces (before adding weatherstrips and trim), the harder it is to close the door. So a rudimentary understanding of mechanics would support the hypothesis that there is a causal relationship. Other industrial processes are not always as obvious as these simple examples, and determination of causal relationships may require more extensive experimentation (Design of Experiments).
Simple Regression Analysis
While Correlation Analysis assumes no causal relationship between variables, Regression Analysis assumes that one variable is dependent upon: A) another single independent variable (Simple Regression) , or B) multiple independent variables (Multiple Regression).
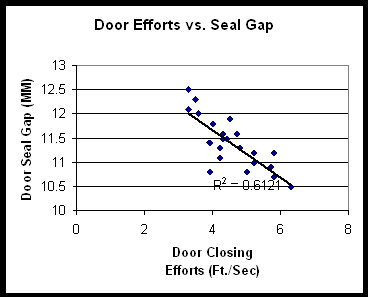
Regression plots a line of best fit to the data using the least-squares method. You can see an example below of linear regression using the same car door scatter plot:
You can see that the data is clustered closely around the line, and that the line has a downward slope. There is strong negative correlation expressed by two related statistics: the r value, as stated before is, -0.78 the r² value is therefore 0.61. R², called the Coefficient of Determination, expresses how much of the variability in the dependent variable is explained by variability in the independent variable. You may find that a non-linear equation such as an exponential or power function may provide a better fit and yield a higher r² than a linear equation.
These statistical calculations can be made using Excel, or by using any of several statistical analysis software packages. MoreSteam provides links to statistical software downloads, including free software.
Multiple Regression Analysis
Multiple Regression Analysis uses a similar methodology as Simple Regression, but includes more than one independent variable. Econometric models are a good example, where the dependent variable of GNP may be analyzed in terms of multiple independent variables, such as interest rates, productivity growth, government spending, savings rates, consumer confidence, etc.
Many times historical data is used in multiple regression in an attempt to identify the most significant inputs to a process. The benefit of this type of analysis is that it can be done very quickly and relatively simply. However, there are several potential pitfalls:
- The data may be inconsistent due to different measurement systems, calibration drift, different operators, or recording errors.
- The range of the variables may be very limited, and can give a false indication of low correlation. For example, a process may have temperature controls because temperature has been found in the past to have an impact on the output. Using historical temperature data may therefore indicate low significance because the range of temperature is already controlled in tight tolerance.
- There may be a time lag that influences the relationship - for example, temperature may be much more critical at an early point in the process than at a later point, or vice-versa. There also may be inventory effects that must be taken into account to make sure that all measurements are taken at a consistent point in the process.
Once again, it is critical to remember that correlation is not causality. As stated by Box, Hunter and Hunter: "Broadly speaking, to find out what happens when you change something, it is necessary to change it. To safely infer causality the experimenter cannot rely on natural happenings to choose the design for him; he must choose the design for himself and, in particular, must introduce randomization to break the links with possible lurking variables".¹
Returning to our example of door closing efforts, you will recall that the door seal gap had an r² of 0.61. Using multiple regression, and adding the additional variable "door weatherstrip durometer" (softness), the r² rises to 0.66. So the durometer of the door weatherstrip added some explaining power, but minimal. Analyzed individually, durometer had much lower correlation with door closing efforts - only 0.41.
This analysis was based on historical data, so as previously noted, the regression analysis only tells us what did have an impact on door efforts, not what could have an impact. If the range of durometer measurements was greater, we might have seen a stronger relationship with door closing efforts, and more variability in the output.
For a more detailed discussion, consult the Statistics Handbook section, or see the book by Box, Hunter and Hunter (recommended).
1. George E. P. Box, William G. Hunter and J. Stuart Hunter, Statistics for Experimenters - An Introduction to Design, Data Analysis, and Model Building (John Wiley and Sons, Inc. 1978) Page 495.
Summary
The regression analysis tool is an advanced tool that can identify how different variables in a process are related. The regression tool will tell you if one or multiple variables are correlated with a process output. This information can identify where in the process control is needed or what factors are the best starting point for a process improvement project.
Additional Resources
Recorded Webcast: "The Transactional Dilemma: Understanding Regression with Attribute Data"
Recorded Webcast: "The Power and the Pitfalls of Multiple Regression Analysis, Part 1"